Quantum Mechanics without the maths or philosophy

Quantum mechanics is normally presented to the popular audience as a philosophical overview that doesn't really teach what quantum mechanics is. When physics undergraduates are taught it, it's presented mathematically, as it should, which unfortunately excludes most interested non physicists.
The aim here is to explain what quantum mechanics is, without falling into either of these traps. It will be presented as a series of points. The reader's aim should be to understand each point. If you're confused, read on - it may be that you can skip points entirely. On the other hand, there's a limit to what can be explained intuitively using animations. I'm going to plough through anyway. Enjoy.

Point 1: Equations say how the curve moves.

Quantum mechanics is based around one key equation: the Schrödinger equation. To understand it, let's first look at other equations in the same family.

Water wave

If you aren't familiar with the mathematics, the equation looks daunting. However, the only thing you need to understand here is that we have an equation on the left, and a behaviour on the right. The behaviour here is a wave that moves in a similar way to the way that a water wave moves. - The behaviour should be intuitively familiar, even if the equation isn't.

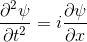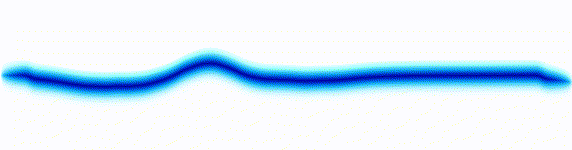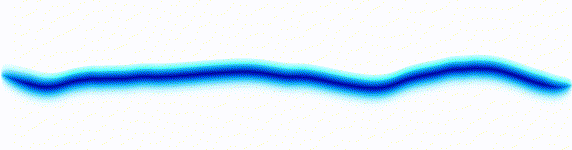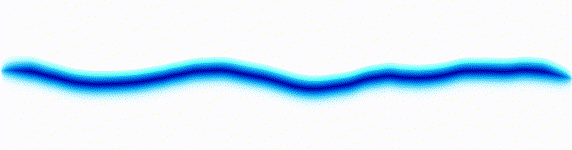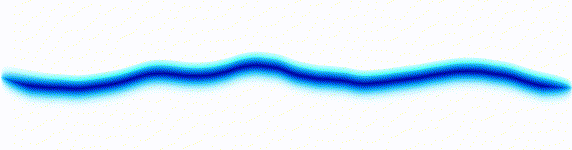Sound wave

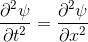On the left there is an equation. On the right, there is a wave that moves in a particular way - in this case, similarly to how a sound wave travels: The height of the graph here would be the pressure of a sound wave as it travels down a corridor.
The important thing is that on the left we have an equation. On the right, we have a behaviour.
The only thing to understand here is that each equation describes the behaviour of a wave. If you change the equation slightly, the way the wave moves is slightly different.

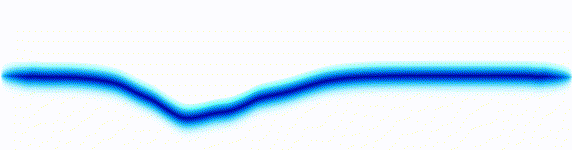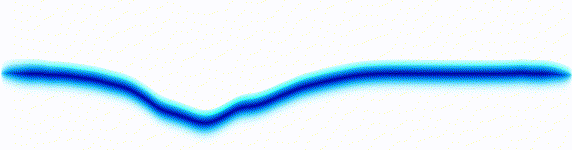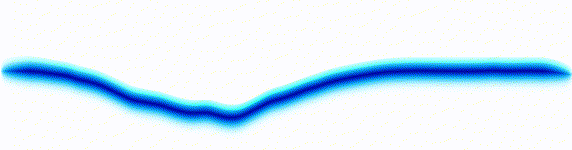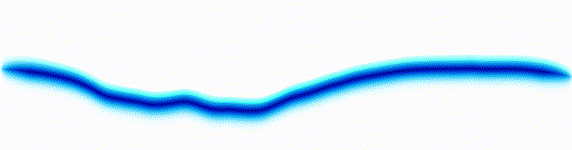
Schrödinger equation

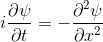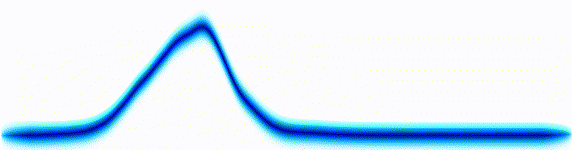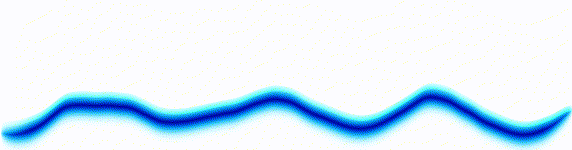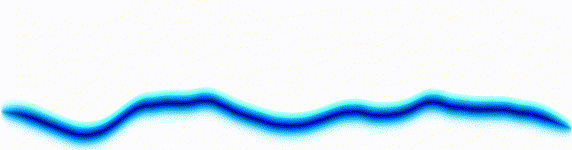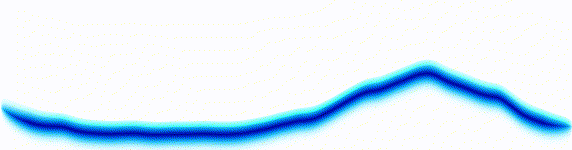Following the pattern, the Schrödinger equation is on the left, and on the right we have a curve that moves in a particular way. It isn't the same way that water moves, and it isn't the same way that a sound wave moves, but it is quite simple.
Summary
Equations of this type describe how a curve moves. The Schrödinger equation is a simple equation, similar to a water wave equation or a sound wave equation.
The curve plotted on the right is called a wavefunction. (The absolute square of the wavefunction is plotted here.)

Point 2: What is the wavefunction

The wavefunction tells you where an electron is likely to be found. The higher the curve, the more likely you are to find the electron just there.

The less said about this the better - if it's not clear what's going on, play with the experiment until the relationship between the curve drawn on the graph, and the probable location of the electron is clear.
Summary
The wavefunction is the thing to focus on - you know it's a wave, and you know that it moves in a particular way. The thing to understand from this point is that it dictates where the electron would be most likely to be found if you did an experiment that could pinpoint it.

Point 3: Two dimensions.

All the examples above were one-dimensional examples. Let's try a two-dimensional example.
The gif below shows an electron moving freely in a square box. The darker the colour, the more likely the electron would be to be found at that position. Note that the equation on the left, as for all the examples, only tells us how the wavefunction moves - not its initial state: The person setting up the experiment dictates that.
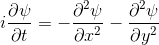In the example above, the electron started off as a probability cloud in the middle, but moving to the right. As time goes on, it spreads out and collides with the walls of its enclosure.
Summary: In the one-dimensional examples, we had a curve that moves in a particular way. It was to be interpreted as the probability of finding the electron at a certain position. In this point, we have a two-dimensional example. Exactly as before, the darkness of the point in the plot indicates the probability of finding the electron at a certain position.

Point 4: Interference

You probably saw above that when the electron collided with the walls of its enclosure, there was an interference pattern that emerged. We can highlight this effect with a simulation of one of the most famous experiments in quantum mechanics: the double slit experiment.
In this experiment, we start off with the electron at the left, moving right. We put a barrier with two slits in its path. Then we see what happens. The pattern you see is interesting because it is seen in actual experiments on single electrons, and it's extraordinarily difficult to come up with a non-wave theory that successfully predicts that single electrons would produce interference patterns.
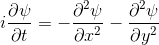If, for instance, you used the theory that an electron moves like a bouncy ball, it wouldn't produce the finger-like patterns.
Summary The theory that electrons move around according to the Schrödinger equation, correctly predicts that you would see interference patterns under some conditions. Our intuitive picture that electrons move around like tiny balls with a definite position and speed, doesn't predict these interference patterns. This pretty much forces people to accept that electrons move like a wave in some sense.

Next Page

---

Other Articles:

---

© Hugo2015. Session @sessionNumber