Generating procedural plants with neural networks

When studying the morphologies of (primitive) plants, it might be helpful to have a semi-plausible model for how different shapes can arise through natural selection. Here's one way to do that using neural networks to grow plants. The advantage of neural networks here is that they can be mutated, and a mutated neural network seems to behave similarly but not identically to the parent - and yet they are a capable of completely general computation.

Another point is that in real life, the growth of organisms depends on networks of proteins: The presence of one protein can stimulate or inhibit the production of other proteins in the same cell, and in some cases, nearby cells. This idea is very similar to how neural networks - each protein maps to each neuron, and each protein interaction maps to a weight in the network. The diffusion of chemicals from one cell to the next is modelled here by neural networks communicating with other networks nearby.

There are lots of ways to generate plants procedurally, but I've chosen to use a neural network that mutates a mesh. You start with a simple mesh, like this:



The next step is to put a vector (type double[15], in these examples) of outputs at every vertex.

At every timestep at every vertex you get the calculation inputs (double[45] here) with three times as many inputs as outputs. This is so the inputs can be the output of (1) this neuron, (2) the average of its neighbours and (3) the difference between its neighbours. All inputs are from the outputs in the previous step.

Some inputs are overwritten with the vertex's position and growth direction.

These outputs are fed into a neural network with 15 outputs, 30 hidden neurons and 45 inputs. Every vertex has an identical neural network.

A simplified diagram looks like this:

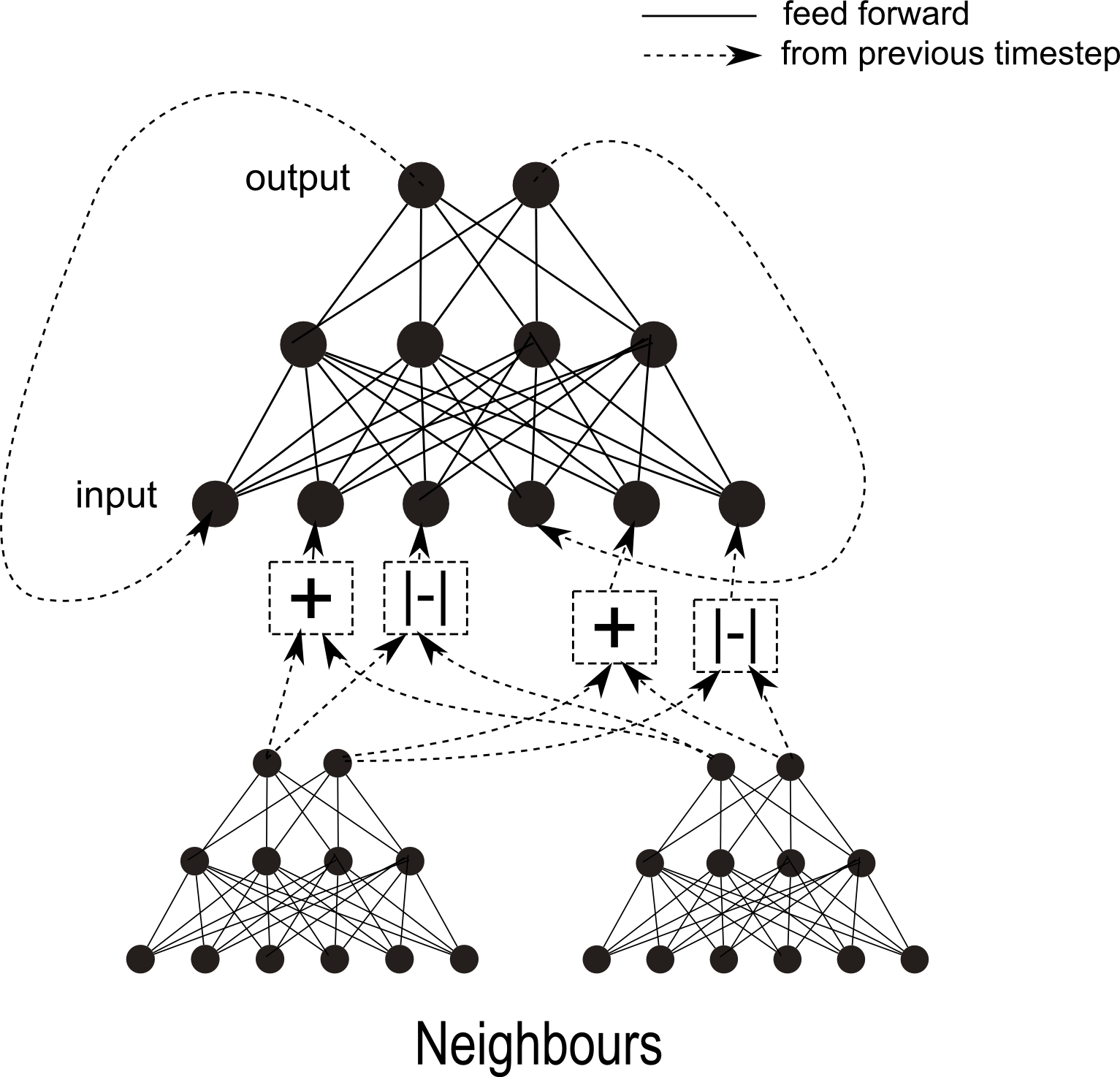
The neural network itself is probably best described with code, since it's fairly simple but a bit fiddly to describe:

  double[] Evaluate(double[] input)
  {
      for (int j = 0; j < input.Length; j++) 
      {
          neuron[0][j].value = input[j];
      }
      for (int i = 1; i < NLayers; i++) // The zero-th layer is skipped.
      {
          for (int j = 0; j < number of neurons in layer i; j++)
          {
                double a = -neuron[i][j].threshold;
                for (int k = 0; k < number of neurons in layer (i-1); k++)
                {
                    a += (neuron[i - 1][k].value - 0.5) * neuron[i][j].weights[k];
                }
                neuron[i][j].value = 1.0 / (1.0 + Exp(-a));
          }
      }
    
      for (int j = 0; j < number of neurons in final layer; j++)
      {
          output[j] = neuron[last][j].value;
      }
      return output;
}

The next step is to grow the mesh. In each timestep, after the vertex outputs have been calculated, you move each vertex according to the outputs.

Each vertex has a growth direction. The distance it moves in each timestep is an increasing function of one of the outputs. If any face grows too large, then a new vertex is placed in its centre, and given a growth direction that is a combination of the normal of the face and also the outputs of the three parent vertices (since all faces have 3 vertices) - so the growth direction of new vertices can be controlled by the neural network.

The final step is to occasionally retriangulate the mesh so that you don't have too many long thin faces. This needs to be done with some care to preserve the overall structure of the object.

This shows what the growing plant looks like:



If you randomise the neural network and grow a plant from it many times, then you get a group of plants like this:



This provides quite a lot of different meshes, which is good, but they are all quite blob-like. The next step is to search for neural networks that are more interesting.

A genetic algorithm can be used to select shapes that optimise a heuristic: Heavily selected meshes tend to be more interesting, and they should lend a sense of correctness to the game: The simulated game world would presumably have competition between plants, so a mesh that competes well is more correct for the game.

The algorithm starts with a population and generates child neural networks from high-fitness parents using mutation and sometimes crossover.

The worse neural networks (according to whether the plant that they grow has a high score) are replaced with the child. In this way the space of possible neural networks is gradually searched for interesting meshes.

If I draw the highest scoring plant in each generation according to maximising horizontal area above a certain height, I get this:

Conclusion

This seems to be a simple way to generate plants procedurally. The method is very flexible: The resulting meshes are in no way constrained by the imagination of the person generating them, because the mesh is entirely driven by a neural network: It's not stitching together different hand-made meshes for instance. The meshes don't have too many polygons either: just a hundred or so for most plants.

The method also makes it easy to generate different meshes with a realistic phyllogeny. For the game Iota Persei it makes sense to generate the meshes this way since it gives underlying reasons for the shapes to be as they are. In the future it might be possible for the player to try to genetically modify plants to see what happens. It's vaguely plausible that in a sci-fi universe plants genuinely could grow with a set of replicating identical neural networks, which also fits with the game's aim.

The work in this article is described in more detail on the preprint arxiv: https://arxiv.org/abs/1603.08551. The source code is part of the submission and you can download it as part of a compressed file that is on the arxiv website.

If you have found this useful, or want to use the code or technique, please do. A reference to the arxiv paper or a link to this project would be appreciated.

---

---

Other Articles:

---

© Hugo2015. Session @sessionNumber