The Double Slit Experiment And Observers

This follows on from a previous article on quantum mechanics that is designed to show the reader how QM works without maths or philosophy here. This time, I'll point out the philosophical problems towards the end.

Lots of people get confused about the role of an intelligent observer in quantum mechanics.

Most experiments and simulations end with a measurement. The electron travels as a wave, but at the end of the experiment, we see where it is. The problem is what we mean by "we see where it is". Does it have to be a person who sees where the electron is?
Another question is as follows: Quantum mechanics is "complete", in the sense that the Schrödinger equation describes the atoms and electrons in the experiment, the measuring device, the eye and the brain. But the Schrödinger equation doesn't have anything in it that can really measure where the electron is. People wonder, then, if consciousness is special or different, or if the Schrödinger equation needs some addition to it to make it realistic, or if the Schrödinger equation only applies to single electrons, or small numbers of electrons.
The answer is pretty much no: The Schrödinger equation by itself is enough to explain all of the phenomena we've ever observed experimentally.

Anyway, I'm going to show you firstly what the double slit experiment is, and then what it looks like when there's an observer.
Let's consider the experiment without an observer.

Point 1. The double slit experiment with a normal ball: perfect knowledge.

We set up an arena for the electron to move around in that looks like this:

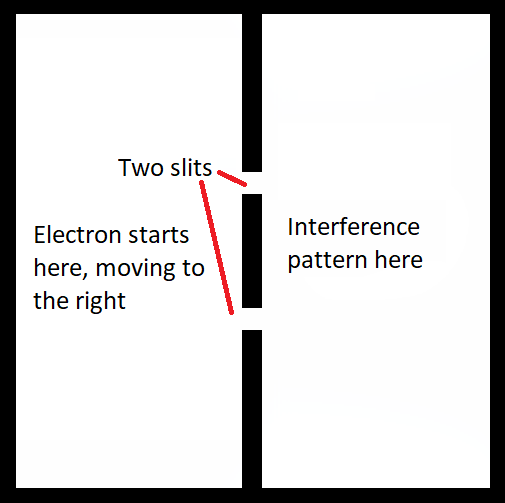The electron is free to move in an arena with walls. A barrier with two openings in it restricts movement between the left and right.

Let's first consider a classical experiment. The electron is now just an ordinary ball, bouncing around our arena:

The ball bouces around, and eventually moves to the other side.

Point 2. The double slit experiment with a normal ball: probability wave

Let's imagine that I don't tell you exactly where the ball is, so you have to guess the probability at each position. One way to do that is to follow 500 hypothetical balls. You don't know which one is actually where the real ball is, but the real ball is more likely to be found in a region with lots of hypothetical balls.

You can see it's sort-of like a wave, but there's no interference pattern.

Point 3. The double slit experiment with an electron

Now we'll do the same with an electron. The difference between a ball and an electron is that an electron is much lighter, and so its wave-like nature is much more obvious. When we do the same experiment as above, we actually get something like this:

(For a fuller explanation of what this kind of diagram means, read this.)

Here is the arena after an electron is added, and allowed to move freely.

Point 4: The double slit experiment with a ball and a detector

Here's the experiment with a ball. The detector flips state when it detects the ball. The detector isn't perfect, but whatever.

So far so good.

Next, let's ask the following pointless deepity:

"Is it really the same arena when the ball has been detected?"

Perhaps there are really two universes, and instead of the detector changing state, we're actually transported to an alternate universe where the detector has detected. Like this:

This is now much more similar to how we have to model the problem in quantum mechanics:

Point 5: The double slit experiment with an electron and a detector