Maths Exam
| 1. | Solution of linear equations
|
| 2. | Differentiation A
|
| 3. | Differentiation A
|
| 4. | Differentiation B
|
| 5. | Integration
|
| 6. | Integration
|
| 7. | Consider the following differential equation: $$ (-\frac{d^2y}{dx^2}) + 2\frac{dy}{dx} - y = 0 $$
|
| 8. | Consider the following series: $$ \sum_{j=0}^{14} 3\left(j - 3\right) $$
|
| 9. | Solution of linear equations
|
| 10. | Differentiation A
|
Other Articles:
|
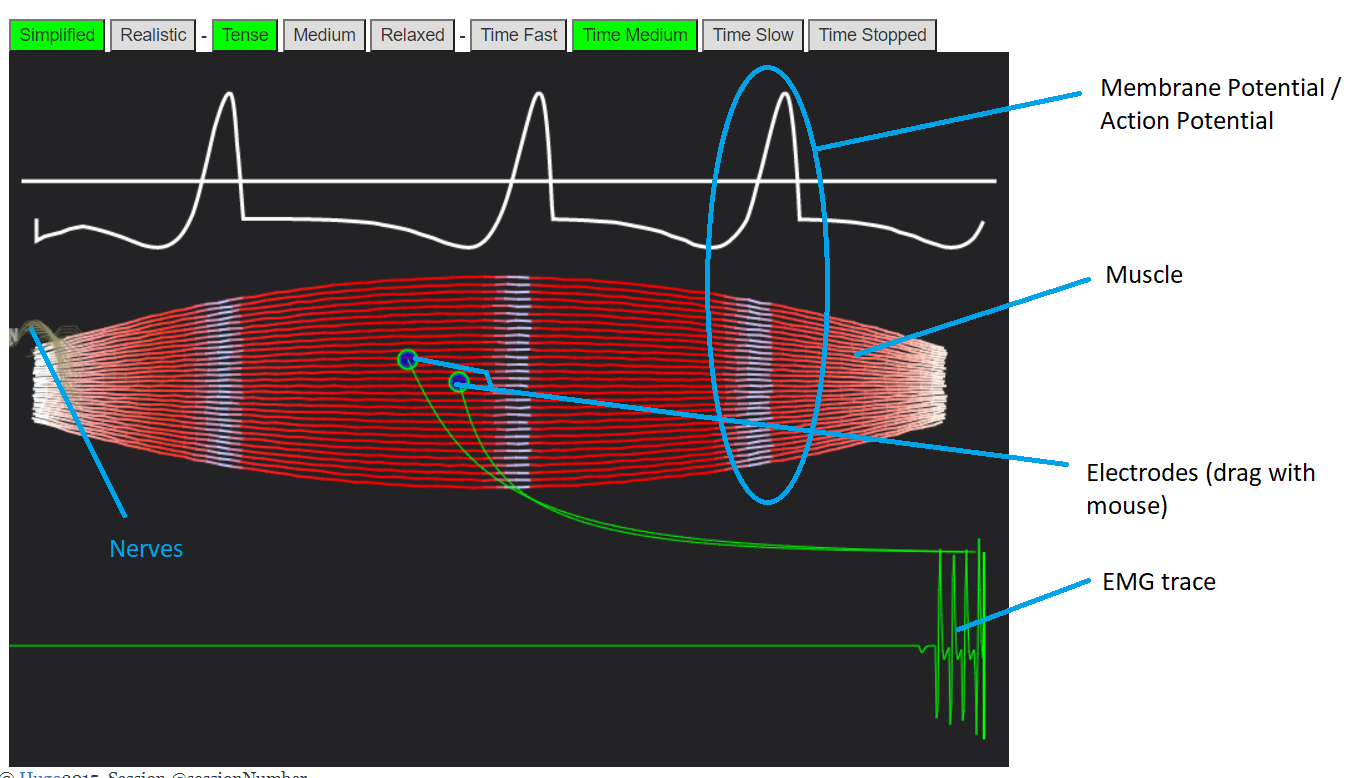
BodyWorks: Neuromuscular Activity / Muscle EMGAn interactive simulation showing how nerves travel to and down muscles, and how this gets picked up by EMG sensors. |
Three Crystal StructuresA ThreeJS model of three crystal structures |

|
